Defining Spheres and Rays
The first step in ray tracing steric hindrance is to define the molecule as a set of spheres with given radii, and to define the rays as a number of vectors emanating (evenly) from a given location.
To define the spheres with which the rays interact, atom_access first shifts the
cartesian coordinates of the molecule such that the atom interest is centred at the origin.
Then, each atom is assigned a spherical radius from a list of known van der Waals atomic radii.[1]
Finally, we discard all atoms whose spheres have no intersection with a spherical region of radius \(r_\text{cutoff}\)
centered on the central atom from the subsequent ray tracing process.
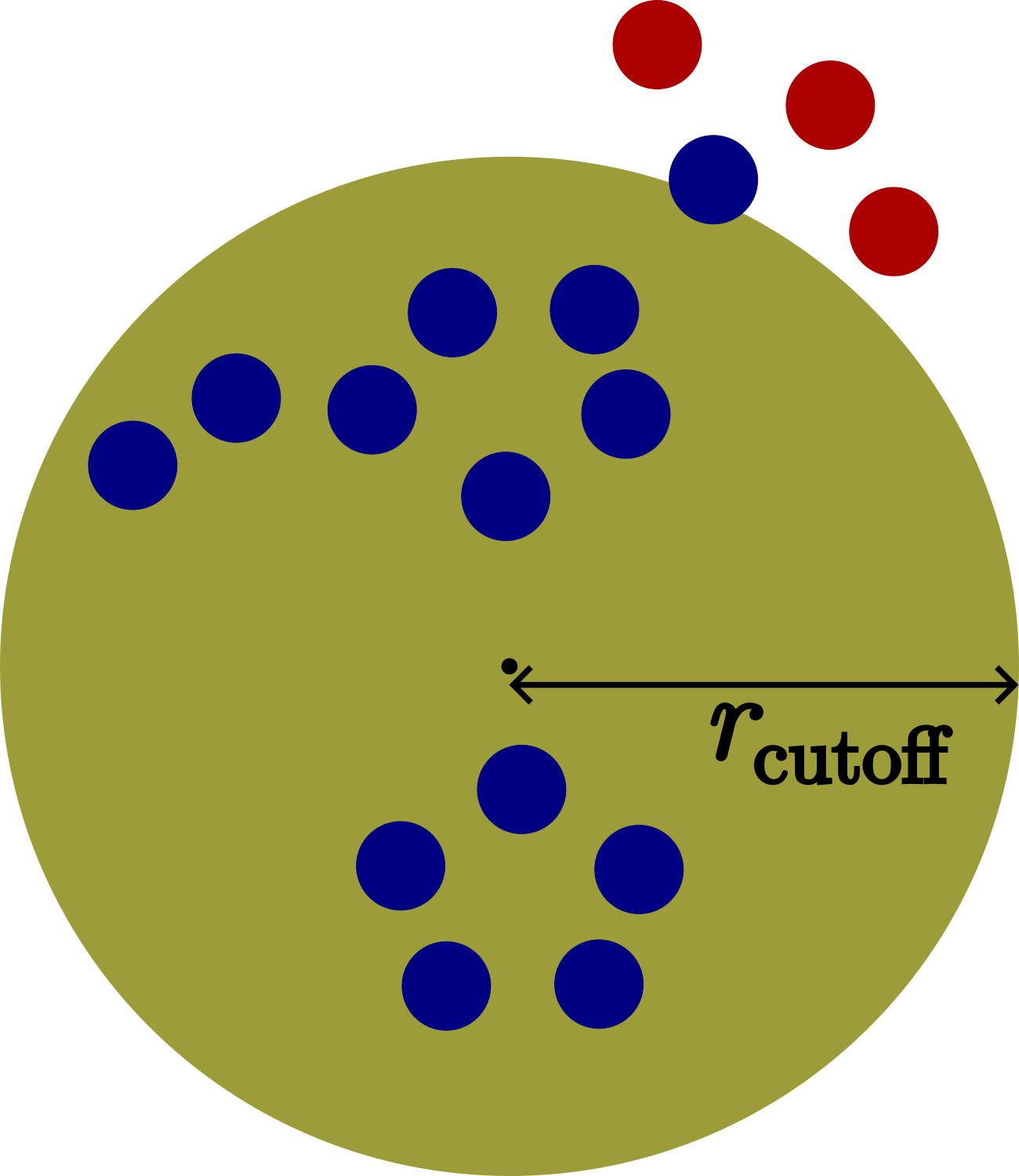
Appliation of the cutoff radius \(r_\text{cutoff}\). Blue atoms lie (at least partially) within the green cutoff sphere and are included in their entirety, while red atoms lie completely outside the cutoff sphere. The black dot signifies the origin, which is the atom of interest.
An angular Zaremba-Conroy-Wolfsberg (ZCW) grid with variable density index \(\rho\),[2][3][4] is used to define a set of rays emanating from the origin (atom of interest) which almost evenly sample the surface of a sphere. The number of rays is controlled by the density index, as given in Table 1.
ZCW density index \(\rho\) |
Number of rays |
|---|---|
0 |
21 |
1 |
34 |
2 |
55 |
3 |
89 |
4 |
144 |
5 |
233 |
6 |
377 |
7 |
610 |
8 |
987 |
9 |
1597 |
10 |
2584 |
11 |
4181 |
12 |
6765 |
13 |
10946 |
14 |
17711 |
15 |
28657 |