Ray Tracing
With the spheres (atoms) and rays defined, atom_access then performs a ray tracing procedure to find accessible sites at
the specified atom of interest.
The Ray-Sphere Interaction Method
The intersection of a ray with a sphere can be found using the Ray-Sphere interaction method (Figure 1), which consists of the following steps.
Consider the interaction of a single unit-ray \(\hat{\bf{u}}\) which emanates from the origin \(\text{O}\) and may or may not intersect a sphere of radius \(r\), with a centre specified by the position vector \(\vec{\bf{C}}\) (Figure 1). Assuming that the origin is not enclosed within this sphere, we seek to find the intersection point(s) \(p_1\) and \(p_2\) where the ray enters and leaves the sphere, if they exist at all.
The dot product \(p = \hat{\bf{u}} \cdot \vec{\bf{C}}\) defines the projection of \(\vec{\bf{C}}\) onto the ray (Figure S1). If \(p\) is negative, then \(\vec{\bf{C}}\) and \(\hat{\bf{u}}\) are in opposite directions and we immediately conclude that there is no intersection. For rays with positive \(p\), we define the quantity \(d\) as the shortest distance between the centre of the sphere and the ray.
Using Pythagoras’ Theorem
we then have three possibilities
\(d^2 > r^2\) : The ray does not intersect with the sphere
\(d^2 = r^2\) : The ray intersects with the sphere once
\(d^2 < r^2\) : The ray intersects with the sphere twice
In the final two cases, the intersections occur at a distance \(p \pm t\) along the ray, where \(t^2=r^2-d^2\), and so the intersection points \(p_1\) and \(p_2\) are defined by the vector equations
where, if the ray enters and leaves the sphere at the same point, then \(t=0\) and \(p_1=p_2\).
Atom_access calculates both \(p_1\) and \(p_2\), but only the former is retained as this point is closest to the origin.
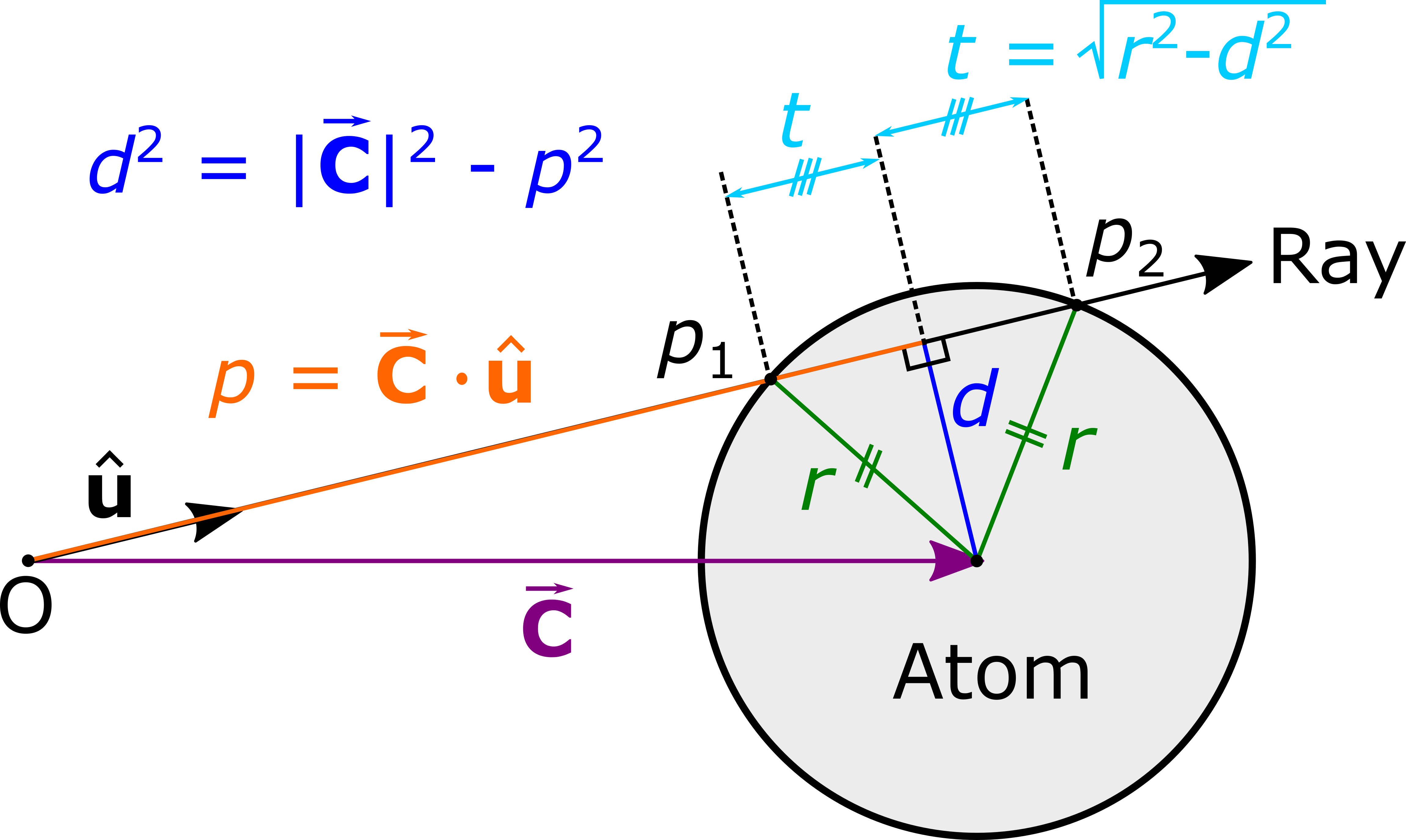
Figure 1: Line-Sphere Interaction Method
Processing the Rays
atom_access carries out the above process, calculating every possible interaction of a given ray with all of the atoms
of a the molecule. Those rays which have no intersections are grouped together as unblocked rays, while those which intersect
with at least one atom are considered to be blocked. The total percentage of unblocked rays is calculated as a fraction of
the total number of rays.